automaton showing interference with each other. There is another
very interesting behaviour (see Fig. 3 a): a wave consisting of
two dispersing one-dimensional excited states periodically creates
an excited block in between. The end points of the blocks become
the starting points of two new waves, which will behave like the
original wave. By this means, the wave is creating a fractal core
inside itself. Figure 3b shows the pattern of a feather which greatly
resembles this fractal core wave. Starting not just with one special
cell but with a few of them, which may~be distributed randomly,
a universe of different and complex patterns can be produced. Among
these patterns there are classes which strongly resemble the frozen
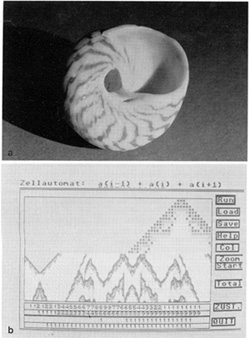
pattern ofthe seashells (see Fig. 4). What is really astonishing
is the major role of the fractals among the pattern in the seashells
(see Fig. 5). For example, the Cymbiolacca shell exhibits a pattern
of brown triangles of different sizes. The way the triangles are
interlocked is typical for patterns of penetrating fractal Sierpinsky
gaskets [13]. 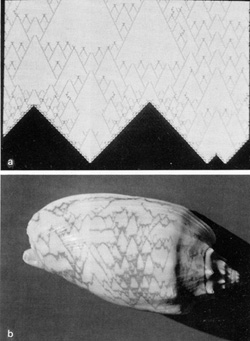
Sometimes one can observe showers of small triangles, while on
other positions the sides of large triangles run through pale yellow-grey
parts of the shell. A book of seashell patterns look like a zoo
of fractal patterns and their combinations, which can be observed
especially on cone shells [14, 15]. Another typical fractal pattern
can be seen in the shell of Conus princeps (Fig. 6). Simulating
this pattern with our automaton machine, it can be classified by
the type ofinterpenetrating core waves which have been mentioned
above. automaton, the pattern of which resembles the main elements
of Cymbiolacca pigmentation Concluding Remarks The regularities and the irregularities in the pattern of the shells
can be reproduced by the automaton model if fractal patterns interact
starting from different positions at time t = O. What is so fascinating
about the fractal patterns? Fractals are strongly related to the
occurrence of deterministic chaos [16], which does not mean that
one loses all regularities but only the simple symmetries such as
translational or rotational symmetry. If all these symmetries break
down in a 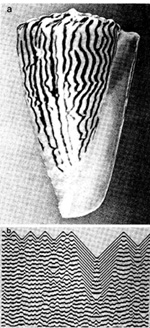
state of chaos, one very characteristic symmetry survives: the
dilatation symmetry, which is mostly disregarded. In the pattern
of the seashells it is precisely this dilatation symmetry which
plays the major role, since all the other symmetries vanished. The
growth mechanism of the pattern proposed above is based on a strictly
ordered one-dimensional arrangement of cells. This is sensible in
the case of the seashells but one can also develop the method for
two- or three-dimensional processes to explain other phenomena in
pure chemical or living systems. Even reaction in fluids can be
modelled in such a way, if the cells stay together for a suitable
period of time [17-19]. It would be of great interest to look for
the spreading of the patterns of excited cells, even in flowing
systems. Acknowledgement. The photograph in Fig. 7a is reproduced
with kind permission of T.F.H. Publication Inc. Ltd., The British
Crown Colony Hong Kong, to whom we are indebted. References 1. Meinhardt H (1984) Models for positional signaling, the threefold
subdivision of segments and the pigmentation patterns of molluscs.
J Embryol Exp Morphol [Suppl] 83:289-311 |