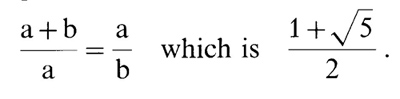|
S. Ohno Beckman Research Institute or the City or Hope, Duarte
California, U.S.A
A. Introduction
It seems as though biologists are extraordinarily fond of randomness.
A population is defined as one, randomly mating, interbreeding unit,
although truly random mating would hardly be practiceable in a reasonably
large population. Similarly, spontaneous mutations are viewed as
randomly sustained base substitutions, in spite of our knowledge
of mutational hot spots. i suspect that this extraordinarily strong
belief in randomness stems from our too strong faith in the power
of natural selection. The unpredictable world of randornness is
the world of chaos. Yet in recent times, there has been increasing
realization that there is order in chaos as well. This realization
started with three equations by Laurenz to describe meteorological
phenomena. No one would dispute the unpredictability of weather.
Yet, these three equations describing heat reflected by the carth
and frictions caused by rotation of the earth revealed the presence
of the strange attractor. The presence of the at tractor, no matter
how strange, is a sure indication of order. Thus, Feigenbaum's conjecture
on chaos came about [1]. There are many different ways of viewing
these developments. Nevertheless, I will present one version pertinent
to the present discussion: the chaotic state is the degenerate form
of the ordered (periodical) state, and this degeneration is due
primarily to progressive step-wise increase of the original periodicity.
Keeping the above in mind, now let us examine the 173-codon-long
chicken lens alfa Acrystallin which is primarily made of ßsheet
structures [2].
B. CCTG Tetramer as the Primordial Repeating Unit of the Crystallin
Coding Sequence
As shown at the top of Fig. 1, this GC rich coding sequence contained
more pyrimidines than purines because of the abundance of C (32.4%).
After this realization, the frequency distribution of Containing
dimers (C X and X C) were obtained. The procedure forced C C dimers
to be overrepresented, for the C C C trimer was counted as 2 C C
dimers. This was because th C C X trimer C C A, e.g., had to be
counted as a 1 C C and a 1 C A dimer. if C C C was regarded as 1
C C dimer, the recurrence rate of the C C dimer is reduced to 47
X. Since all sequences, no matter how short, are translatable by
three reading frames, 1/3 of them should serve as Pro codons C C
X. This predicts the presence of 16 Pro (9";;, ) in this protein.
Indeed, there were 14 Pro residues. Next to C C, the more frequently
recurring C-containing dimers were T C (41 X), C T (39 X), and C
A (39 X). The above suggested relative abundance of Ser and Leu
but not of Gin and His, for 1/3 of 39 C AX are to be split evenly
between Gin codons C A G, C ;\ A, and the His codons C A C and C
A T. indeed, there were 5 Gin and 6 His residues. The very fact
that the amino acid composition of the protein is fairly predictable
by recurrent rates of base dimers in its coding sequence immediately
places in grave doubt the conventional wisdom of genes
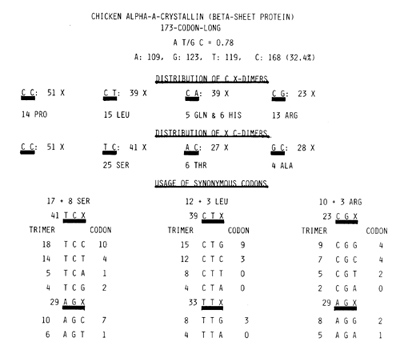
Fig. I. At the top, the AT/GC ratio and base composition
of the 519-base-Iong chicken ClA-crystallin coding sequence [2]
are given, followed by the recurrent ratcs of C X and X C dimers.
The rate for the C C dimer is an overestima1e for the reason given
in the text. In the case of Leu, GIn, His, and Thr, the recurrence
of a relevant dimer divided by 3 gives a resonable estimation of
the number of amino acids. At the bottom, 6 codons each for Ser,
Leu, and Arg are shown in three vertical columns. The recurrent
rates of each as a trimer and as a codon are shown. In each instance,
the most preponderant among the synonymous codons also recurred
most frequently as the base trimer
evolving by natural selection operating upon individual codons.
Indeed, three columns at the bottom of Fig. 1 show that with regard
to Ser, Leu, and Arg, encodable by 6 codons each, preponderant among
the synonymous codons sharing the first two bases invariably is
the one that recurred most frequently as base trimer. Thus, codon
usages too are determined merely by recurrent rates of pertinent
base trimers. Figure 1 and data not shown also suggested that the
most frequently recurring base tetra mer should be C C T G. This
was due to the fact that the 21 X recurring trimer C C T and the
15 X recurring C T G overlap with each other. Indeed, C C T G was
the most frequently recurring base tetramer; 9 X recurrence (Fig.
2). This tetramer was translated in all three different reading
frames to encode two Pro, five Leu, and one each of Trp and Cys.
As might be deduced from Fig. 1, the next most frequently recurring
base tetramer was 7 X recurring T C T Cas shown boxed in Fig. 2.
T C T C, however, can be regarded as two successive T C dimers.
Nevertheless, this tetramer would soon be mentioned again. How significant
was the 9 X recurrence of C C T G? The expected recurrence rate
of this tetra mer can be computed in two different ways. If based
upon the 15 X recurrent rate of C T G,
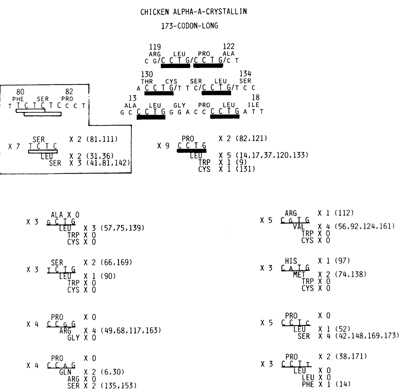
Fig.2. C C T G as the primordial heptamer is underlined by
the thick solid bar. It recurred 9 X and was translated in three
different reading frames as shown in the upper center stage. In
its 1st reading frame. it encoded 2 Pro (the positions of these
Pro in the amino acid sequence are shown in parentheses), 5 Leu
in its 2nd, and 1 each of Trp and Cys in its 3rd reading frames
Shown at the top are three pairs of C C T G that recurred in succession.
Placed inside the box at the Ieft is the 2nd most frequently recurring
base tetramer T C T C that recurred 7 X. This, however, is a T C
dimer X 2 and in one place a T C dimer recurred three times in succession.
Shown in two columns near the bottom are 8 of the 12 single-base-substituted
derivatives of G C T G that recurred 3 X or more
the expected recurrent rate for C C T G becomes 0.324 x 15 = 4.86.
As shown at the top of Fig. 1, 0.324 of the 519 bases were Cs. If
based upon the 21 X recurrence of the C C T trimer, the expected
recurrence rate of C C T G now becomes 21 xO.237=4.9. Clearly the
9 X recurrence of the C C T G tetramer was not by chance. Due to
single base substitutions affecting one or the other of four positions,
C C T G was expected to yield 12 different kinds of single-base-substituted
derivatives. As shown in the bottom half of Fig. 2, 8 of them recurred
3 to 5 times, while the remainder recurred twice each. It follows
then that not counting several overlapped bases twice, C C T G and
its single-base-substituted derivatives occupied 35% of the entire
coding sequence. It would thus appear that the cxA-crystallin coding
sequence was ultimately derived from C C T G tetrameric repeats
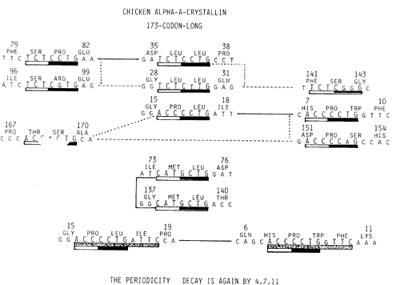
Fig. 3. Shown in the 1st and 3rd rows are two pairs of identical
C C T G containing heptamers, while shown in the 3rd and 4th rows
are each one's respective single-base-substituted copies. Identical
heptamers are connected by the solid line and single-base-substituted
derivatives by broken lines. Those translated in the 1st reading frame
arc shown in the left column, while the center column contains those
translated in 2nd reading frame, and the right column those in 3rd
reading frame. Two identical G C T G-containing heptamers, both translated
in the 2nd reading frame, are shown in the 5th and 6th rows, Two identical
heptamers shown in the 3rd row were actually parts of 11-base-long
repeating units as shown at the bottom

Fig. 4. The particular musical transformation given to the
recurring heptamer A C C C C T G according to the set rule previously
put forward [5]
that existed in the prebiotic world of eons ago [3]. Three consecutive
copies of C C T G should have given the tetrapeptidic periodicity
Pro-Ala-Cys-Leu to the original peptide chain. Indeed, the 120th
and 121st Leu-Pro of the chicken (XA-crys tall in were still encoded
by two consecutive copies of C C T G as shown at the very top of
Fig. 2. As the periodicity decayed in the periodic-to-chaotic transition,
the original exact tetrameric periodicity should have yielded to
longer and


f'ig.5a, b. The musical transformation based on the melodic
heptamer (Fig. 4) of 7th to 48th codons of the chicken IXA-crystallin
coding sequence [2]
longer less exact periodicities. Indecd, two pairs of C C T G shown
near the top of Fig. 2 were now separated by 3 and 5 bases.
C. Periodicity Decay by the Golden Mean: the 3,4,7,11,18 Rule
Of the consecutive numbers the first four are 1, 2, 3,4. At this
point, we begin to add previous two numbers to obtain the next number;
i.e., 3+4=7. If we keep doing this, the series of numbers form:
3, 4,7,11, 18, 29,47, 76,123, etc. Now we divide 7 by 4,11 by 7,18
by 11, and so on. Then we see that results begin to approach 1.618
and reach that goal at 123 divided by 76, and remains 1.618 forever
thereafter. Now, 1.618 is the well-known golden ratio expressed
as
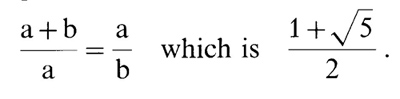
In a previous paper, we have shown that the periodicity decay in
coding sequences is according to the above-noted golden mean [4].
Of the nine C C T G tetramers, two recurred in immediate succession
of each other as shown in Fig. 2. The remaining seven, on the other
hand, recurred as parts of recurring heptamers. Two such pairs are
shown in f'ig. 3, because members of each pair are translated in
different reading frames. Shown at the top row of Fig. 3 are two
identical copies of the heptamer T Z C T C C T G, yielding the 80th
and 81st SerPro when translated in the first reading frame, while
encoding Leu-Leu dipeptide in the second reading frame. A pair of
single-base-substituted copy T C T C G G G; the translation of this
heptamer in its third reading frame encoding the 141st to 143rd
Phe-Ser-Gly. It is pointed out that each of these five heptamers
( one identical pair and a triplet derived from that pair) contained
the second most frequently recurring base tetramer T C T C already
noted. Thus, five of the 7 X recurring T C T C combined with the
most frequently recurring tetramer C C T G and its derivatives to
become parts of recurring heptamers. Shown in the third row of Fig.
3 are another identical pair of C C T G-containing heptamers A C
C C T G encoding the 16th and 17th Pro- Leu in its second reading
frame, while encoding the seventh to tenth His-Pro- Trp in its third
reading frame. This identical pair of heptamers on the one hand
yielded its single-base-substituted derivatives (Fig. 3, fourth
row) while, on the other hand, becoming parts of the pair of 11base-long
repeating units that differed from each other by a single-base substitution
(Fig. 3, bottom row). Thus, the periodicity decay by the chicken
lens ClAcrystallin coding sequence is indeed according to the golden
mean: 4, 7, 11 rule. Needless to say, single-base-substituted derivatives
of the primordial heptamer C C T G have often become parts of the
identical pair of heptamers. One such G C T G-containing pair of
identical heptamers encoding a pair of Met-Leu dipeptides of the
74th,75th and 138th and 139th positions is shown in the fifth and
sixth rows of Fig. 3. When modern coding sequences are analyzed
in the above manner, one can not help but realize that natural selection
operating upon individual codons has mainly contributed to the conservation
of a fait accompli by eliminating function-depriving, therefore,
deleterious mutations. But this had very little to do with the initial
acquisition of functions by proteins encoded by ancestral coding
sequences of eons ago. For this, I contend that the universal principle
of periodic-to-chaotic transition is responsible.
D. Musical Transformation of the 7th to 48th Codons of the Chicken
alfa A-Crystallin Coding Sequence
Some time ago, I came to the realization that the periodic-to-chaotic
transitional state of modern coding sequences can best be appreciated
by their musical transformation under the set rule [5]. The 5' region
of the 519-base-Iong chicken (XA-crystallin coding sequence [2]
is the domain ruled by the heptamers A C C C C T G and T C T C C
T G as shown in Fig. 3. By giving the melody shown in fig. 4 to
the former, the 7th to 48th codons of this coding sequence have
been transformed to the musical composition for piano shown in Fig.
5 a and b ). By listening to it, one can readily realize the periodicity
decay by the 4,7,11,18 rule. E. Summary and Conclusions Modern coding
sequences are in the periodic-to-chaotic transition. In the case
of (XA-crystallin coding sequence of the chicken, the initial tetrameric
periodicity of the primordial tetramer C C T G has been decaying
by the golden mean: the 4, 7,11 rule. Thus, the tetramer has become
parts of recurring heptamers, and some heptamers have become parts
of the 11base-long repeating units.
References
1 Feigenbaum MJ (1985) The universal metric properties of nonlinear
transformations. J Stat Physics 21:669-706
2. Okazaki KM, Yasuda K, Kondoh H, Okada TS (1985) DNA sequences
responsible for tissue-specific expression of a chicken alpha-crystalling
gene in mouse lens cells. EMBO J 4:2589-2595
3. Ohno S (1987) Evolution from primordial oligomeric repeats to
modern coding sequences. J Mol Evol 25:325-329
4. Ohno S (1988) Codon preference is but an illusion created by
the construction principle of coding sequences. Proc Natl Acad Sci
USA 85 ff
5. Ohno S, Ohno M (1986) The all pervasive principle of repetitious
recurrence governs not only coding sequence construction but also
human endeavor in musical composition. Immunogenetics 24: 71- 78
|